Grafos

Um grafo é uma representação abstrata de um conjunto de objetos e das relações existentes entre eles. É definido por um conjunto de nós ou vértices e pelas ligações ou arestas, que ligam pares de nós. Uma grande variedade de estruturas do mundo real podem ser representadas abstratamente através de grafos.

Conceitos de grafos

Um grafo é descrito por um par (V,E), onde V é o conjunto de vértices e E o conjunto das arestas que ligam pares de vértices. Um grafo pode ser dirigido ou direcionado, se as arestas tiverem uma direção, ou não dirigido, se as arestas não tiverem direção. A figura seguinte ilustra um grafo dirigido.

Se as arestas tiverem associado um peso ou custo, o grafo passa a chamar-se de grafo pesado. A figura seguinte ilustra um grafo pesado não dirigido.

Os nós podem ser de diferente tipos, representados por cores ou etiquetas. Nesse caso, o grafo diz-se colorido. A figura seguinte ilustra um grafo colorido não dirigido.

Quando apenas é admitida no máximo uma aresta entre dois nós, diz-se que o grafo é simples.

Grafos e a Ciência de Computadores

Com a enorme utilidade dos grafos, existe toda uma área de Ciência de Computadores dedicada ao seu estudo e são inúmeros e muito importantes os algoritmos que manipulam grafos. Um exemplo é o Algoritmo de Dijkstra, que encontra o caminho mais curto entre um nó e todos os outros nós, num grafo pesado. Existem muitos outros algoritmos para outras tarefas tais como maximizar o fluxo entre nós ou encontrar a árvore mínima de suporte.

Do ponto de vista da Programação, um grafo é uma estrutura de dados e existem duas maneiras base de o implementar na prática:

• Matriz de Adjacências: uma matriz de V por V células, onde a célula na linha i e coluna j nos dá informação sobre a ligação entre os nós i e j. Por exemplo, se o grafo não for pesado, a célula podia conter o valor verdadeiro (ou um) quando existisse uma ligação entre i e j e o valor falso (ou zero) quando tal não acontecesse. Se o grafo for pesado, cada célula pode conter um número representando o peso da aresta. A figura seguinte ilustra um grafo não dirigido e a sua correspondente matriz de adjacências.

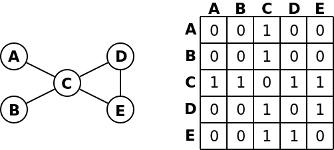
• Lista de Adjacências: um vetor de listas onde a posição i do vetor contém uma lista dos nós aos quais o nó i se encontra ligado. Se o grafo for pesado, cada elemento da lista contém também o peso da ligação. A figura seguinte ilustra um grafo não dirigido e a sua correspondente lista de adjacências.

A matriz permite verificar em tempo constante se uma dada ligação existe ou não. Por oposição, no caso da lista, tal não acontece e é necessário percorrer a lista para saber se um dado nó está ou não ligado. Em contrapartida, se for necessário percorrer todos os nós ligados a um dado nó, a lista é mais eficiente, pois permite percorrer apenas os nós ligados, e não andar a percorrer toda uma linha da matriz, verificando se a ligação existe ou não.